Kelvin functions
In applied mathematics, the Kelvin functions Berν(x) and Beiν(x) are the real and imaginary parts, respectively, of
where x is real, and 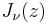 is the νth order Bessel function of the first kind. Similarly, the functions Kerν(x) and Keiν(x) are the real and imaginary parts, respectively, of
is the νth order Bessel function of the first kind. Similarly, the functions Kerν(x) and Keiν(x) are the real and imaginary parts, respectively, of 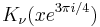 , where
, where 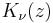 is the νth order modified Bessel function of the second kind.
is the νth order modified Bessel function of the second kind.
These functions are named after William Thomson, 1st Baron Kelvin.
While the Kelvin functions are defined as the real and imaginary parts of Bessel functions with x taken to be real, the functions can be analytically continued for complex arguments x ei φ, φ ∈ [0, 2π). With the exception of Bern(x) and Bein(x) for integral n, the Kelvin functions have a branch point at x = 0.
Contents |
Ber(x)
For integers n, Bern(x) has the series expansion
where 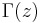 is the Gamma function. The special case Ber
is the Gamma function. The special case Ber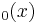 , commonly denoted as just Ber(x), has the series expansion
, commonly denoted as just Ber(x), has the series expansion
![\mathrm{Ber}(x) \sim \frac{e^{\frac{x}{\sqrt{2}}}}{\sqrt{2 \pi x}} [f_1(x) \cos \alpha %2B g_1(x) \sin \alpha] - \frac{\mathrm{Kei}(x)}{\pi}](/2012-wikipedia_en_all_nopic_01_2012/I/103fba31788dc52e9033701096767b34.png) ,
,
where 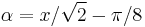 , and
, and
Bei(x)
For integers 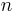 , Bei
, Bei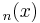 has the series expansion
has the series expansion
where 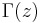 is the Gamma function. The special case Bei
is the Gamma function. The special case Bei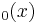 , commonly denoted as just Bei
, commonly denoted as just Bei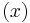 , has the series expansion
, has the series expansion
and asymptotic series
![\mathrm{Bei}(x) \sim \frac{e^{\frac{x}{\sqrt{2}}}}{\sqrt{2 \pi x}} [f_1(x) \sin \alpha - g_1(x) \cos \alpha] - \frac{\mathrm{Ker}(x)}{\pi}](/2012-wikipedia_en_all_nopic_01_2012/I/db3b8148b8d5c03dc0621659dfa6f1a9.png) ,
,
where 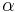 ,
, 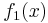 , and
, and 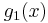 are defined as for Ber
are defined as for Ber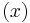 .
.
Ker(x)
For integers n, Kern(x) has the (complicated) series expansion
where 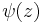 is the Digamma function. The special case Ker
is the Digamma function. The special case Ker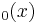 , commonly denoted as just Ker
, commonly denoted as just Ker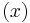 , has the series expansion
, has the series expansion
and the asymptotic series
where 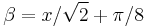 , and
, and
Kei(x)
For integers n, Kein(x) has the (complicated) series expansion
where 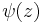 is the Digamma function. The special case Kei
is the Digamma function. The special case Kei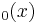 , commonly denoted as just Kei
, commonly denoted as just Kei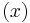 , has the series expansion
, has the series expansion
and the asymptotic series
where 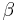 ,
, 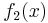 , and
, and 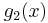 are defined as for Ker
are defined as for Ker .
.
See also
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 9", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 379, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_379.htm.
- Olver, F. W. J.; Maximon, L. C. (2010), "Bessel functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/10
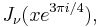
![\mathrm{Ber}_n(x) = \left(\frac{x}{2}\right)^n \sum_{k \geq 0} \frac{\cos\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right]}{k! \Gamma(n %2B k %2B 1)} \left(\frac{x^2}{4}\right)^k](/2012-wikipedia_en_all_nopic_01_2012/I/8da04b6acc18f14e5fba726585e2816b.png)
![\mathrm{Ber}(x) = 1 %2B \sum_{k \geq 1} \frac{(-1)^k (x/2)^{4k}}{[(2k)!]^2}](/2012-wikipedia_en_all_nopic_01_2012/I/7c7799c404ad6e0261d5613a7da033ed.png)
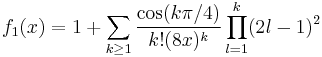
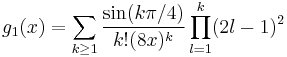
![\mathrm{Bei}_n(x) = \left(\frac{x}{2}\right)^n \sum_{k \geq 0} \frac{\sin\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right]}{k! \Gamma(n %2B k %2B 1)} \left(\frac{x^2}{4}\right)^k](/2012-wikipedia_en_all_nopic_01_2012/I/e6e5256531fbb9f9cab28a3d5bbd0e38.png)
![\mathrm{Bei}(x) = \sum_{k \geq 0} \frac{(-1)^k (x/2)^{4k%2B2}}{[(2k%2B1)!]^2}](/2012-wikipedia_en_all_nopic_01_2012/I/4f8797b75b1ff5c1ea2d4e2bc28ac43f.png)
![\begin{align}
\mathrm{Ker}_n(x) & = \frac{1}{2} \left(\frac{x}{2}\right)^{-n} \sum_{k=0}^{n-1} \cos\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right] \frac{(n-k-1)!}{k!} \left(\frac{x^2}{4}\right)^k - \ln\left(\frac{x}{2}\right) \mathrm{Ber}_n(x) %2B \frac{\pi}{4}\mathrm{Bei}_n(x) \\
& {} \quad %2B \frac{1}{2} \left(\frac{x}{2}\right)^n \sum_{k \geq 0} \cos\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right] \frac{\psi(k%2B1) %2B \psi(n %2B k %2B 1)}{k! (n%2Bk)!} \left(\frac{x^2}{4}\right)^k
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/e2e9adfc1fee5fadc41dcfc2a94f281a.png)
![\mathrm{Ker}(x) = -\ln\left(\frac{x}{2}\right) \mathrm{Ber}(x) %2B \frac{\pi}{4}\mathrm{Bei}(x) %2B \sum_{k \geq 0} (-1)^k \frac{\psi(2k %2B 1)}{[(2k)!]^2} \left(\frac{x^2}{4}\right)^{2k}](/2012-wikipedia_en_all_nopic_01_2012/I/e072a3d7474d633e5165881dcb2b9fdd.png)
![\mathrm{Ker}(x) \sim \sqrt{\frac{\pi}{2x}} e^{-\frac{x}{\sqrt{2}}} [f_2(x) \cos \beta %2B g_2(x) \sin \beta],](/2012-wikipedia_en_all_nopic_01_2012/I/721f5d99a7d6283e0d0559c83ae795bf.png)
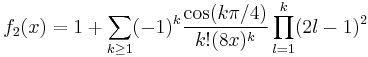
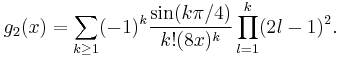
![\mathrm{Kei}_n(x) = -\frac{1}{2} \left(\frac{x}{2}\right)^{-n} \sum_{k=0}^{n-1} \sin\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right] \frac{(n-k-1)!}{k!} \left(\frac{x^2}{4}\right)^k - \ln\left(\frac{x}{2}\right) \mathrm{Bei}_n(x) - \frac{\pi}{4}\mathrm{Ber}_n(x) %2B \frac{1}{2} \left(\frac{x}{2}\right)^n \sum_{k \geq 0} \sin\left[\left(\frac{3n}{4} %2B \frac{k}{2}\right)\pi\right] \frac{\psi(k%2B1) %2B \psi(n %2B k %2B 1)}{k! (n%2Bk)!} \left(\frac{x^2}{4}\right)^k](/2012-wikipedia_en_all_nopic_01_2012/I/c326eceb6d2f14afe617565ed48231c5.png)
![\mathrm{Kei}(x) = -\ln\left(\frac{x}{2}\right) \mathrm{Bei}(x) - \frac{\pi}{4}\mathrm{Ber}(x) %2B \sum_{k \geq 0} (-1)^k \frac{\psi(2k %2B 2)}{[(2k%2B1)!]^2} \left(\frac{x^2}{4}\right)^{2k%2B1}](/2012-wikipedia_en_all_nopic_01_2012/I/993a98c47760c90835b1a8f289b3756b.png)
![\mathrm{Kei}(x) \sim -\sqrt{\frac{\pi}{2x}} e^{-\frac{x}{\sqrt{2}}} [f_2(x) \sin \beta %2B g_2(x) \cos \beta],](/2012-wikipedia_en_all_nopic_01_2012/I/afcbe322ab043c648b2b9502db0a2701.png)